[Introduction to Reinforcement Learning with David Silver] #2. MDP

Introduction to MDPs

Introduction to MDPs

1. 마르코프 결정 과정(MDP)는 강화학습에서 환경을 묘사한다.
2. 환경이 완전 관측 가능한 경우에 사용
3. 거의 모든 강화학습의 문제는 MDP로 표현할 수 있다.
   • continuous MDP의 최적화 문제
   • Partially observable(부분 관측 문제)도 MDP로 변환할 수 있다.

※ 마르코프 결정과정(MDP)는 MP(Markov Process), MRP(Markov Reward Process)의 확장이다

MP, MRP, MDP

 

마르코프 과정(MP, Markov Process)

마르코프 특성(Markov Property)

• 마르코프(Markov)는 19~20세기 러시아의 수학자 ‘안드에리 마르코프’를 뜻함. 마르코프 과정을 통해 복잡한 확률과정을 단순한 가정으로 접근
• 마르코프 과정(Markov Property) : St+1은 직전 St에만 영향을 받고, 그 이전 S1,S2, …, St-1과는 통계적으로 독립이다.
• 즉, 어떤 상태(St+1)가 되기 위한 확률은 직전 상태(St)에만 의존한다.
  • 다음 상태에 대한 확률 값이 직전 과거에만 종속
  • 따라서, 과거(History)에 대한 정보와는 무관
• “The future is independent of the past given the present”
  • 미래는 과거와 독립적(independent)이다.

A Condition of Markov

상태전이 매트릭스(State Transition Matrix)

• 상태 전이 확률(State Transition Probability)는 현재 상태(S)에서 다음 상태(S’)으로 전이될 확률을 의미한다.
• 상태 전이 매트릭스(State Transition Matrix)는 상태 전이 확률을 행렬로 나타낸 매트릭스로 행렬의 행의 합은 1이다.
  • 예) SUM(P11, … , P1n) = 1
  • 상태 S1에서 어떤 상태던 다음 상태로 넘어가야 하기 때문에 다음 상태(Sx)로 전이될 확률(P1x)을 모두 더하면 1이 되어야 한다.
• 그림에서 스마일 에이전트가 현재 상태(S)에서 우측(벽) 상태(St+1)으로 전이될 상태 전이 확률은 0일 것이다. (벽으로 막혀있기 때문에)

마르코프 과정(Markov Process)

• 마르코프 과정(Markov Process)는 경로와 관계없이(memoryless) 랜덤한 과정이다.

• 마르코프 과정(Markov Process)는 상태(S)와 상태 전이 확률 매트리스(P)로 구성된다. <S, P>

마르코프 체인 예시

An Example of Markov Chain

 

• 학생이 왼쪽의 마르코프 체인을 따른다고 가정하자.
• 상태 : 상태는 총 6개(Facebook, Class1, Class2, Class3, Pass, Pub, Sleep)이다.
• 상태전이확률 : 상태전이확률은 상태와 상태를 연결하는 화살표의 값이다.
  • 예 : Class1에서 Class2로 전이될 상태전이 확률(P)는 0.5이다.
• 이 경우 다양한 에피소드 샘플(Sample)을 추출할 수 있다.
  • C1 C2 C3 Pass Sleep
  • C1 C2 C3 Pub C2 C3 Pass Sleep

 

마르코프 보상 과정(MRP, Markov Reward Process)

마르코프 보상 과정(MRP)

• 마르코프 보상(리워드) 과정 은 마르코프 체인(Markov Chain or Markov Processs)에 가치(Value)가 추가된 것을 의미한다.
• MRP에서 보상(Reward, R)은 에이전트가 상태(S)에서 받을 것이라 예상되는 기댓값이다.
  ※ MDP에서의 보상과 다르다. (MDP에서는 행동(Action)에 대한 내용이 추가된다.)
• 감가율(r)은 현재에 가까운 상태에 대한 보상을 더크게 평가하기 위하여 미래의 보상에 대해서는 감가율을 적용하여 더 낮게 평가한다.
  • 예 : 현재 상태에서 100만큼 보상이 예상되고 다음 상태에서도 100만큼 보상이 예상될때, 감가율이 0.9라고 가정
    • 현재 상태의 보상 기댓값 = 100
    • 다음 상태의 보상 기댓값 = 100 * 감가율(0.9) = 90

Definition of Markov Reward Process

마르코프 보상 과정(MRP) 예시

An Example of MRP

• 보상(R)이 추가된 Markov Chain 예시로 적색으로 표시된 보상값이 해당 상태에서 얻을 것이라 예측되는 보상이다.
  • 예 ) Pass 상태에 도달할시에 학생의 목표를 달성한 것이 되므로 Pass 상태에 도달시 보상으로 10을 받는것으로 설정
• 좌측 그림에서 감가율은 생략된 상태임

반환값(Return)

Definition of Return

• 반환값(Return, Gt)은 에이전트가 t에서부터 얻을것이라 예상되는 보상의 합이다.
• 감가율(r)이 적용되어 현재의 보상이 미래의 보상보다 더 큰 가치를 갖도록 함
  • 감가율이 0에 가까울수록 근시적인(myopic) 평가
  • 감가율이 1에 가까울수록 미래를 내다보는(far-sighted) 평가

예) 에피소드가 t=1부터 3까지 진행했다고 가정시 반환값

• 감가율을 적용하는 이유수학적으로 편리하다. (Mathematically convenient)
• 무한으로 반복(cyclic)하는 것을 피할 수 있다.
• 불확실한(Uncertainty) 미래는 완전하게 표현할 수 없다.
• 보상이 금전적인 것이라 가정했을때, 현재의 보상이 더 많은 이자를 가져온다.
  • 현재의 재화가치가 미래의 재화가치보다 높다는 것과 유사
• 인간과 동물의 행동은 즉각적인 보상을 선호한다.

MRP에서의 가치함수(Value Function)

Value Function of an MRP

• MRP에서 가치 함수는 상태(S)에 대한 가치(long-term value)를 의미한다.
• 가치 함수는 상태(S)에서 시작하여 얻게 되는 반환값의 기댓값이다.

MRP에서 반환값/가치함수 예시

• 학생(에이전트)이 C1에서 시작(S1=C1)해서 C1 C2 C3 Pass Sleep으로 진행되었다고 가정했을때 가치함수(v1)는 -2.25이다. (* 감가율 =0.5)
  • $R_2(C1) = -2 $ / $ R_3(C2) = -2 $
  • $R_4(C3) = -2 $ / $ R_5(Pass) = 10 $

MRP에서 벨만 방정식 (Bellman Equation for MRPs)

• 가치함수는 두 파트로 나눌 수 있다.
  • 즉각적인 보상 ($R_{t+1}$)
  • 다음 상태의 가치함수에 감가율을 곱한 값 ($ \gamma \, v(S_{t+1}) $)
• 따라서 보상함수를 보상($R$)과 상태전이확률($P$)로 표현할 수 있다.

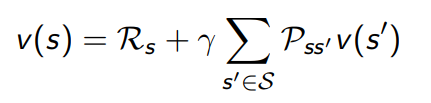
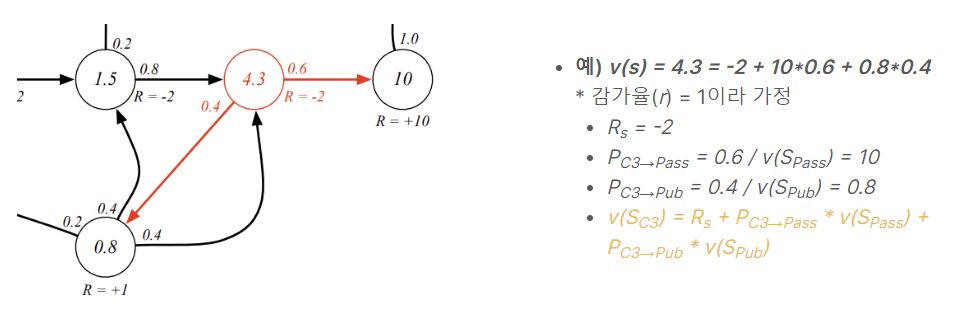
MRP에서 벨만 방정식을 통한 가치함수 계산 예시

마르코프 결정과정(MDP, Markov Decision Process)

마르코프 결정과정(Markov Decision Process)

• 마르코프 결정 과정(MDP)은 마르코프 보상과정(MRP)에 결정(decision)이 추가된다.
  • 결정을 하기 위한 행동(A, Action)이 추가된다.
  • 행동(A)는 에이전트가 어떤 상태(S)에서 실행 가능한 활동을 의미한다.
    • 예를 들어, grid한 환경에서 에이전트가 상,하,좌,우로 움직일수 있다면 상,하,좌,우의 움직임이 행동이 된다.
• 모든 상태(S, States)가 마르코프(Markov)한 환경(Environment)을 의미한다.
• 상태 전이 확률(매트리스)과 보상함수도 행동에 관한 내용이 추가된다.
  • 상태 전이 확률 : 상태(s)에서 행동(a)를 했을때 다음상태(s’)이 될 확률
  • 보상 : 상태(s)에서 행동(a)를 했을때의 보상값의 기대값

정책(Policy)

• 정책이란 에이전트가 어떤 상태(s)에서 행동(a)을 할 확률을 의미한다.
• 따라서 정책은 에이전트의 행동을 정의한다.
  • 예를 들어 상하좌우로 움직이는 로봇이 있을시에 상하좌우로 움직일 확률을 모두 동일하다고 정책을 설정하면 다음과 같다.
    • $ \pi(a = left |s) = 0.25 $
    • $ \pi(a = right |s) = 0.25 $
    • $ \pi(a = up |s) = 0.25 $
    • $ \pi(a = down |s) = 0.25 $
• MDP에서 정책은 히스토리가 아닌 현재 상태에 의존한다.

MDP에서의 가치함수(Value Function)

• 가치함수는 상태에 대한 가치를 평가하는 상태 가치함수와 행동에 대한 가치를 평가하는 행동 가치함수로 구분된다.

벨만기대방정식(Bellman Expectation Equation)

• 벨만 기대 방정식(Expectation Equation)은 가치함수에 대하여 방정식으로 표현
• 상태가치함수와 행동가치함수에 대하여 표현

최적가치함수(Optimal Value Function)

• 최적가치함수는 최적 상태 가치함수와 최적 행동 가치함수가 있다. 
• 최적 상태 가치함수는 상태 가치함수 값이 최대가 되는 정책을 선택한다.
• 최적 행동 가치함수는 행동 가치함수(Q함수) 값이 최대가 되는 정책을 선택한다. 

최적정책(Optimal Policy) & 벨만 최적 방정식(Bellman Optimality Equation)

※ 해당 내용은 David Silver 교수님의 Introduction to Reinforcement Learning 강의를 기반으로 강화학습에 대하여 정리한 자료입니다.

• 강의 영상(Lecture) : https://www.youtube.com/watch?v=2pWv7GOvuf0&list=PLqYmG7hTraZDM-OYHWgPebj2MfCFzFObQ
• 강의 슬라이드(Slide) : https://www.davidsilver.uk/teaching/